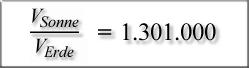Pyramidengröße

Nachdem ich mich ausführlich mit den unterschiedlichen Theorien zur Form der Cheops-Pyramide beschäftigt hatte, tauchte irgendwann die Frage auf: Warum wurden die Pyramiden so gigantisch groß gebaut? Wären sie alle nur halb so groß, so wären sie immer noch riesig und das Volumen würde bei halber Höhe nur noch ein Achtel des tatsächlich realisierten Volumens betragen. Das hätte doch eine Menge Arbeit gespart.

1. Anpassungsfaktoren

In der Literatur fand ich bisher zwei Zusammenhänge, die angeblich die Größe der Cheops-Pyramide festlegen. Zum einen soll der Abstand von der Erde zur Sonne genau das Eine-Milliardenfache der Höhe der Cheops-Pyramide betragen. Zum anderen soll der Abstand zweier Breitenkreise genau 600mal so groß sein, wie die Dreieckshöhe der Seitenflächen der Cheops-Pyramide. Beim ersten Zusammenhang schwankt der Fehler zwischen 0,3 % und 3,6 %. Das liegt daran, dass die Erdbahn kein konzentrischer Kreis um die Sonne ist, sondern eine Ellipse, in deren einem Brennpunkt die Sonne steht. Dadurch schwankt der Abstand von der Erde zur Sonne. Beim zweiten Zusammenhang liegt der Fehler bei ca. 0,5 %, was relativ wenig ist.

Beide Zusammenhänge mögen zunächst interessant klingen, haben jedoch einen gravierenden Nachteil. Beide enthalten einen willkürlichen Faktor, sozusagen einen "Anpassungsfaktor". Im ersten Zusammenhang beträgt der Faktor 1 Milliarde (=1.000.000.000) und im zweiten Zusammenhang 600. Es lässt sich mathematisch relativ leicht zeigen, dass mit solchen Faktoren so ziemlich alles gezeigt werden kann, wie zum Beispiel ein Zusammenhang zwischen der Höhe einer Saturn-V-Rakete und der durchschnittlichen Größe einer Spitzmaus.

Mit zwei beliebigen Größen und einem solchen Faktor erhält man eine Genauigkeit von ungefähr 10 %, wenn man Faktoren zulässt, wie 100, 200, 300, ... , 1000, 2000, 3000, ... , usw.. Das heißt, die Faktoren beginnen mit einer Ziffer und haben eine beliebige Anzahl von Nullen. Die 10 % Genauigkeit lassen sich veranschaulichen, wenn der geforderte Anpassungsfaktor z. B. genau 550 beträgt. In diesem Fall liegt er zwischen den Faktoren 500 und 600. Die Abweichung wäre 50 und damit 10 % von 500. Wenn man jedoch berücksichtigt, dass innerhalb einer Pyramide fünf Längen zur Auswahl stehen (Grundkantenlänge, Diagonale, Höhe, Abstand Spitze-Grundkante und Länge der schrägen Kanten, die zur Spitze verlaufen) und wenn man fünf Vergleichslängen hinzunimmt (Abstand Erde-Sonne, Erdumfang, usw.), so gibt es schon 25 Kombinationsmöglichkeiten. Es bedeutet, dass die Genauigkeit von ca. 10 % bei einem der Zusammenhänge im statistischen Mittel auf ein Fünfundzwanzigstel abnimmt. Das wären nur noch 0,4 %. Das heißt, mit solchen Anpassungsfaktoren, wie z. B. 1 Milliarde oder 600, kann leicht eine Genauigkeit von unter 1 % erreicht werden! Damit ließe sich wirklich alles zeigen, und die Zusammenhänge wären nicht signifikant!

Die klassische Erklärung aus der ägyptologischen Forschung besagt, dass die Höhe der Cheops-Pyramide 280 königliche Ellen beträgt und ihre Grundkantenlänge 440 Ellen. Damit wäre die Größe ebenfalls festgelegt. Doch dies wäre im Grunde keine ausreichende Erklärung für die Größe, sondern die Frage würde sich nur wie folgt ändern: Warum wurde die Cheops-Pyramide 280 Ellen hoch gebaut? 140 Ellen hätten es doch auch getan. Eine weitere Frage wäre, ob nicht eventuell das altägyptische Längenmaß anhand der Grundkanten der schon bestehenden Pyramide nachträglich definiert wurde.

Diese Überlegungen sollten vollständig verstanden werden, damit das Folgende nachvollzogen werden kann. Der wesentliche Aspekt ist, dass willkürliche Anpassungsfaktoren, wie z. B. 600, 700, 800, usw. zu Ergebnissen führen, die nicht signifikant, d. h. im Grunde sinnlos sind. Zum einen dürfen keine Anpassungsfaktoren verwendet werden, zum anderen sollte ein möglicher Zusammenhang aber auch nahe liegend sein. Das heißt, die verwendeten Größen sollten sinnvoll sein und die Gleichung (wenn es eine gibt) eine einfache Form besitzen. Das ist der Ausgangspunkt.


2. Größe der Cheops-Pyramide

Durch Prüfen von Massen, Durchmessern, Bahnradien und Volumina von Sonne, Planeten und Mond, sowie anderen physikalischen Größen wurde ein Zusammenhang gefunden, wobei eine physikalische Konstante ins Spiel kam, die gar nicht vermutet worden war. Die Sonne ist vom Volumen etwa 1,3 Millionen mal größer als die Erde. Das genaue Verhältnis der Volumina von Sonne und Erde wird in vielen Astronomiebüchern als Zahl angegeben. Aus dem dtv-Atlas zur Astronomie, der relativ bekannt sein dürfte, erhalten wir [2] (zitierte Quellen am Ende der Seite "Zusammenfassung"):

Sehr genaue Messdaten zur Großen Pyramide, die wir im folgenden benötigen werden, wurden 1925 von Borchardt und Cole veröffentlicht [3, 4]. Multiplizieren wir nun den Mittelwert der Kantenlängen S = 230,364 m mit dem oben angegebenen Volumenverhältnis der beiden Himmelskörper, so ergibt sich: Das ist alles. Wer sich ein wenig mit der Physik befasst, wird auch ohne Angabe der Lichtgeschwindigkeit erkennen, dass die berechnete Strecke die Entfernung ist, die das Licht in einer Sekunde zurücklegt. Man nennt diese Strecke auch eine Lichtsekunde. Die relative Abweichung beträgt nur 0,03 %. Die Astronomie-Literatur liefert nun nicht immer denselben Wert für obiges Volumenverhältnis, wobei die Abweichungen im Mittel 0,2 % betragen. Dies ändert jedoch grundlegend nichts. Etwas umgestellt erhalten wir den Zusammenhang:

Das Volumenverhältnis Erde zu Sonne ist also gleich dem Verhältnis der Grundkantenlänge S zur Strecke einer Lichtsekunde! Die Gleichung entspricht dem klassischen Dreisatz aus der Mathematik und enthält überhaupt keinen Anpassungsfaktor. Sie ist also denkbar einfach. Bei den beiden Himmelskörpern handelt es sich nicht um den Saturn oder den Pluto, die nicht besonders nahe liegend wären, sondern um die Erde und die Sonne. Beide Himmelskörper ergeben Sinn, da die Sonne unser Zentralstern ist und sich auf der Erde die Pyramiden (und wir selbst) befinden. Ebenfalls gibt es eine interessante Analogie: Im oberen Teil der Brüche (den Zählern) steht das Volumen der Erde und die Grundkantenlänge der Pyramide, im unteren Teil, den Nennern, das Volumen der Sonne und das Licht (Lichtsekunde). Diese Zuordnung erscheint natürlich, da die Pyramide mit ihrer Grundkante auf der Erde ruht und die Sonne natürlich unsere Hauptlichtquelle ist.

Die Lichtgeschwindigkeit und die Volumina von Sonne und Erde sind fundamentale Größen. Eine berechtigte Frage wäre aber die Folgende: Was ist mit der Sekunde? Sie ist in der Strecke einer Lichtsekunde enthalten und scheint doch von Menschen geschaffen worden zu sein. Wäre die Sekunde länger oder kürzer, so würde die Gleichung (1) nicht mehr stimmen. Ist die Sekunde nicht eher eine willkürliche Größe? Dazu gibt es zwei Aspekte: Zum einen ist offenbar nicht bekannt, wer das Zeitmaß "Sekunde" auf diesem Planeten eingeführt hat. Alle Menschen verwenden diese Zeiteinheit, aber niemand weiß warum! Man weiß nur, dass die alten Ägypter schon die Einteilung des Tages in 24 Stunden kannten und dass die alten Babylonier das Sexagesimal-System verwendeten, ein Zahlensystem zur Basis 60. Zum anderen hat der Physiker Eckhard H. Wallenwein ein System bzw. ein Modell entdeckt , welches die Zeiteinteilung in Stunden, Minuten und Sekunden, die Winkeleinteilung in Grad, Bogenminuten und Bogensekunden, das altgriechische Längenmaß "Plethron" (30,83 m) sowie das heutige Längenmaß "Meter" auf sinnvolle Weise in einem gemeinsamen Schema vereint [5]. Er nennt das Modell die "11!-Meter-Erde". Der Ausdruck "11!" – sprich: 11-Fakultät – ist das Produkt der Zahlen 1 bis 11. Und Wallenwein kommt zu dem Schluss, dass man zur Zeit des Alten Ägypten die Sekunde schon kannte. (Es wäre theoretisch sogar möglich, dass der Bau der Großen Pyramide und die Einführung der "Sekunde" gleichzeitig stattfanden.) Dieses Modell wird in seinem Buch "Das Altägyptische Universum" [5] mit zahlreichen weiteren Informationen ausführlich erklärt. Einen kurzen verständlichen Abriss davon mit einigen Ergänzungen, die auch die Cheops-Pyramide betreffen, gibt es in "Pyramiden und Planeten" [6, S. 295 bis 298].


3. Größe der Chefren-Pyramide

Gibt es nun eine ähnliche Gleichung für die zweite große Pyramide, die Chefren-Pyramide? Die Antwort ist "Ja". Der Zusammenhang lautet: Die Volumina der beiden großen Pyramiden stehen im selben Verhältnis zueinander wie die Volumina der Planeten Erde und Venus. Bei dem folgenden Vergleich der Verhältnisse kann die Venus als ideale Kugel, d. h. ohne Abplattung, angesehen werden, da sie nur sehr langsam rotiert.
Wir erhalten für die Pyramiden (V = 1/3 · S^2 · h, S = Grundkantenlänge und h = Pyramidenhöhe) und die Planeten jeweils ein Volumenverhältnis von:

Die Größen zur Bestimmung der Planetenvolumina stammen aus der Datensammlung von K. R. Lang [7]. Die relative Abweichung der Volumenverhältnisse beträgt etwa 0,1 %. Der Zusammenhang lässt sich darstellen als:

Wie auch in Gleichung (1) sind die Größen, d. h. die Volumina V, eindeutig definiert, und es wird kein Anpassungsfaktor verwendet. Wir haben die Zuordnung: Cheops-Pyramide – Erde und Chefren-Pyramide – Venus vor uns. Die Venus ist nicht irgendeiner der übrigen acht Planeten unseres Sonnensystems, sondern liegt auf der benachbarten Planetenbahn zur Sonne hin. Der nächste Nachbar in entgegengesetzter Richtung ist der Mars, welcher jedoch im Durchschnitt um einiges weiter entfernt seine Bahn zieht als die Venus. Das heißt, die Gleichung ist im wahrsten Sinne des Wortes nahe liegend.


4. Größe der Mykerinos-Pyramide

Es fehlt uns jetzt nur noch eine Beziehung für die dritte Pyramide. Das Interessante ist, dass die Erde der dritte Planet und die Venus der zweite Planet im Sonnensystem ist. Der erste Planet ist der Merkur, welcher deutlich kleiner als die beiden anderen Planeten ist. Ist die Mykerinos-Pyramide, welche ebenfalls kleiner als die anderen beiden Pyramiden ist, dem Merkur zuzuordnen? Dann würden die drei großen Pyramiden in ihrer Reihenfolge genau den ersten drei Planeten unseres Sonnensystems entsprechen. Ersetzt man nun in der Gleichung (2) die Volumina von Chefren-Pyramide und Venus durch die Volumina von Mykerinos-Pyramide und Merkur, so müsste die Grundkante der dritten Pyramide 89,1 m lang sein. Tatsächlich beträgt die Länge ca. 105,5 m und wäre damit um 18 % zu groß. Es hat einige Zeit gedauert, bis der dritte Zusammenhang gefunden wurde.

Dafür müssen wir uns vorweg die Planetenbahnen etwas genauer ansehen. Die Planeten bewegen sich um die Sonne nicht auf Kreisbahnen sondern auf Ellipsenbahnen. Hierbei befindet sich der Zentralkörper (die Sonne) nicht genau in der Mitte der Ellipse, sondern in einem der beiden Brennpunkte. Diese Tatsache hat erstmals Johannes Kepler in seinem ersten "Keplerschen Gesetz" formuliert. Es bedeutet, dass die Planeten sich manchmal näher zur Sonne bewegen und manchmal weiter weg stehen. (Dies ist auf der Erde übrigens nicht der Grund für die Jahreszeiten. Letzteres wäre theoretisch möglich, doch die Erdbahn hat annähernd Kreisform, so dass dieser Effekt sehr gering ist. Die Jahreszeiten beruhen auf der Neigung der Erdachse zur wechselnden Sonnenrichtung.) Den nahesten Punkt der Planetenbahn zum zentralen Himmelskörper nennt man Perihel und den entferntesten Aphel (siehe Abbildung 2.2). Die Entfernung von der Sonne zum Aphel, d. h. die Apheldistanz, wird mit Q bezeichnet. Nach diesem kleinen astronomischen Ausflug kommen wir wieder zur dritten Pyramide. Der astronomische Zusammenhang, der die Größe der Mykerinos-Pyramide festlegt, lautet wie folgt: Das heißt, die Grundkantenlängen S von Cheops- und Mykerinos-Pyramide stehen im selben Verhältnis zueinander, wie die Apheldistanzen Q bei Erde und Merkur. Wir erhalten erneut die Zuordnung Cheops-Pyramide zu Erde und diesmal Mykerinos-Pyramide zu Merkur. Der Fehler ist mit ca. 0,2 % etwas größer, als bei den anderen beiden Gleichungen. Er ist jedoch erklärbar, da die Grundkanten der Mykerinos-Pyramide ursprünglich gar nicht endgültig bearbeitet worden waren, so dass deshalb für die Grundkantenlänge eine gewisse Unsicherheit besteht. Diese Beziehung würden genau in das Bild der anderen beiden Gleichungen passen.
 
Zum Nachrechnen für den Leser: Die Grundkantenlängen von Mykerinos- und Cheops-Pyramide betragen im Mittel 105,501 m [1] und 230,364 m [3, 4]. Die Apheldistanzen von Merkur bzw. Erde zur Sonne sind 0,46669 AE und 1,0167 AE. Die Abkürzung AE bedeutet „Astonomische Einheit“ und ist die durchschnittliche Entfernung Erde – Sonne.
 
Aber wenn dem so ist - warum wurden ausgerechnet die Aphelentfernungen gewählt und nicht die Volumina wie bei Erde und Venus? Auch wenn die Wahl der Planeten sinnvoll wäre und die Genauigkeit der Gleichung (ohne Anpassungsfaktor) weit über einen Zufall hinausreicht, möchte ich an dieser Stelle nicht behaupten, dass die Aphelentfernungen besonders nahe liegend sind. Wenn die drei großen Pyramiden von Gizeh die drei ersten Planeten unseres Sonnensystems - Merkur, Venus und Erde - repräsentieren sollen, wäre es nicht nahe liegender gewesen, alle drei Volumina der Pyramiden proportional zu den Planetenvolumina abzustimmen? Dann wäre die Zuordnung eindeutig gewesen. Was ist so besonders an der Aphelentfernung?
 
Bevor dies beantwortet wird, schauen wir uns noch einmal die drei Gleichungen (1) bis (3) an. Allen drei Gleichungen liegt der mathematische Dreisatz zugrunde. In allen drei Gleichungen wird die Cheops-Pyramide der Erde zugeordnet. Des weiteren haben wir die Zuordnungen: Chefren-Pyramide zur Venus, Mykerinos- Pyramide zum Merkur und Sonne zum Licht. Keine der drei Gleichungen enthält einen willkürlichen Anpassungsfaktor, was es enorm schwierig macht, einen solchen Zusammenhang zwischen beliebigen Größen herzustellen.

Die Frage, ob diese Zusammenhänge überhaupt korrekt sind, stellt sich gar nicht. Die Gleichungen sind mit der angegebenen Toleranz von ca. 0,1 % bis 0,2 % natürlich korrekt. Die Frage, die sich vielmehr ergibt, ist die nach dem Zufall: Handelt es sich bei diesen Zusammenhängen um Zufall oder nicht? Hierzu müsste man die Wahrscheinlichkeiten dafür abschätzen, dass es sich bei den Feststellungen um Zufall handelt oder nicht. Das ist in der Physik z. B. in der Quantenmechanik eine alltägliche Sache. Die Überlegungen, die in "Pyramiden und Planeten" ausführlicher dargestellt sind [6, S. 87 bis 92], würden hier jedoch zu weit führen. Das Ergebnis lautet: Die Wahrscheinlichkeit, dass die Zusammenhänge (inklusive weiterer, hier nicht aufgeführter Aspekte) alle gleichzeitig zufällig passen, ist vergleichbar mit der Wahrscheinlichkeit für einen Hauptgewinn im Lotto - also sehr sehr gering.

Das wesentliche Ergebnis, das wir im folgenden benötigen werden, ist, dass die drei großen Pyramiden in Gizeh in der Reihenfolge Mykerinos-, Chefren- und Cheops-Pyramide, den inneren drei Planeten unseres Sonnensystems zuzuordnen sind, nämlich Merkur, Venus und Erde. Und damit können wir diesen zunächst hypothetischen Zusammenhang genauer untersuchen.

 Nach oben │ Impressum u. Datenschutz │ English Version